Profit and Loss Aptitude for RRB
ssc preparation, important competetion questions, current affairs of india, latest question asked in competetion papers,
Profit and Loss Aptitude PDF
In this we have given Profit & Loss Aptitude Notes Pdf for those who are preparing for Competitive Examination. This, we believe shall be useful in preparing and gearing up for taking the exams.
Cost Price: The amount paid to purchase an article or the price at which an article is made, is known as its cost price. The cost price is abbreviated as C. P.
Selling Price: The price at which article is sold, is known as its selling price.
The selling price is abbreviated as S. P.
Download RRB JE Study Material
Profit: If the selling price (S.P.) of an article is greater than the cost price (C.P), then the difference between the selling price and cost price is called profit.
Thus, If S. P. > C.P., then
Profit = S. P. – C. P.
⇒ S. P. = C. P. + Profit
⇒ C. P. = S. P. – Profit.
Loss: If the selling price (S.P.) of an article is less than the cost price (C.P.), then the difference between the cost price (C.P.) and the selling price (S.P.) is called loss.
Thus if S.P. < C.P., then
Loss – C.P. – S.P.
⇒ C. P. = S. P. + Loss
⇒ S. P. = C. P. – Loss
Example 1:
An article was brought for Rs 2000 and sold for Rs 2200. Find the gain or loss.
Solution:
C.P. of the article = ` 2000
S.P. of the article = ` 2200
Since S.P. > C.P. So there is gain.
Gain (profit) = S. P. – C. P.
= ` 2200- ` 2000= ` 200
An article was brought for Rs 2000 and sold for Rs 2200. Find the gain or loss.
Solution:
C.P. of the article = ` 2000
S.P. of the article = ` 2200
Since S.P. > C.P. So there is gain.
Gain (profit) = S. P. – C. P.
= ` 2200- ` 2000= ` 200
Profit and loss percentage
The profit per cent is the profit that would be obtained for a C.P. of `100.
Similarly, the loss per cent is the loss that would be made for a C.P. of ` 100.
The profit per cent is the profit that would be obtained for a C.P. of `100.
Similarly, the loss per cent is the loss that would be made for a C.P. of ` 100.
REMEMBER
Profit = (C.P.×Profit%)/100
Loss = (C.P.×Loss%)/100
S.P. = ((100+Profit%)/100) × C.P.
S.P. = ((100-Loss %)/100) × C.P.
C.P. = (100×S.P.)/(100+Profit%)
C.P. = (100×S.P.)/(100-Loss %)
Loss = (C.P.×Loss%)/100
S.P. = ((100+Profit%)/100) × C.P.
S.P. = ((100-Loss %)/100) × C.P.
C.P. = (100×S.P.)/(100+Profit%)
C.P. = (100×S.P.)/(100-Loss %)
Example 2:
A cycle was purchased for Rs 1600 and sold for Rs 1400. Find the loss and loss %.
Solution:
C.P. of the cycle = Rs 1600
S.P. of the cycle = Rs 1400
Since S.P. < C.P., so there is a loss.
Loss = C.P. – S.P.
= Rs 1600 – Rs 1400 = Rs 200.
Loss % = Loss/(C.P.) ×100= 200/1600×100=121/2%
A cycle was purchased for Rs 1600 and sold for Rs 1400. Find the loss and loss %.
Solution:
C.P. of the cycle = Rs 1600
S.P. of the cycle = Rs 1400
Since S.P. < C.P., so there is a loss.
Loss = C.P. – S.P.
= Rs 1600 – Rs 1400 = Rs 200.
Loss % = Loss/(C.P.) ×100= 200/1600×100=121/2%
Example 3:
By selling a table for Rs 330, a trader gains 10%. Find the cost price of the table.
Solution:
S.P. = Rs 330, Gain = 10%
∴C.P. = (100/(100+Gain %))×S.P.
=Rs 100/(100+10)×330
=100/110×330=Rs 300
By selling a table for Rs 330, a trader gains 10%. Find the cost price of the table.
Solution:
S.P. = Rs 330, Gain = 10%
∴C.P. = (100/(100+Gain %))×S.P.
=Rs 100/(100+10)×330
=100/110×330=Rs 300
Example 4:
A sells a bicycle to B at a profit of 20% and B sells it to C at a profit of 25%. If C pays `225 for it, what did A pay for it.
Solution:
C.P. of A= 225× 100/(100+20)×100/(100+25)
=225×100/120×100/125=Rs 150.
A sells a bicycle to B at a profit of 20% and B sells it to C at a profit of 25%. If C pays `225 for it, what did A pay for it.
Solution:
C.P. of A= 225× 100/(100+20)×100/(100+25)
=225×100/120×100/125=Rs 150.
Example 5:
A mobile phone is sold for Rs 5060 at a gain of 10%. What would have been the gain or loss per cent if it had been sold for Rs 4370?
Solution:
S.P. = Rs 5060, gain = 10%
∴C.P. =(5060×100)/(100+10)=Rs 4600.
2nd S.P. = Rs 4370
Since, S.P. < C.P., so there is loss.
∴Loss % = ((4600-4370)×100)/4600 = 5%
If a man buys x items for Rs y and sells z items for Rs w, then the gain or loss percent made by him is (xw/zy-1)×100%
A mobile phone is sold for Rs 5060 at a gain of 10%. What would have been the gain or loss per cent if it had been sold for Rs 4370?
Solution:
S.P. = Rs 5060, gain = 10%
∴C.P. =(5060×100)/(100+10)=Rs 4600.
2nd S.P. = Rs 4370
Since, S.P. < C.P., so there is loss.
∴Loss % = ((4600-4370)×100)/4600 = 5%
If a man buys x items for Rs y and sells z items for Rs w, then the gain or loss percent made by him is (xw/zy-1)×100%
Example 6:
Some articles were bought at 6 for Rs 5 and sold at 5 for Rs 6. Gain percent is:
Solution:
Suppose, number of articles bought = L.C.M of 6 and 5 = 30
C.P. of 30 articles = Rs (5/6×30)=25
S.P. of 30 articles = Rs (5/6×30)=36
Gain % = (11/25×100)%=44%
Some articles were bought at 6 for Rs 5 and sold at 5 for Rs 6. Gain percent is:
Solution:
Suppose, number of articles bought = L.C.M of 6 and 5 = 30
C.P. of 30 articles = Rs (5/6×30)=25
S.P. of 30 articles = Rs (5/6×30)=36
Gain % = (11/25×100)%=44%
Shortcut method:
Quantity Price
6 5
5 6
% profit = (xw/yz-1)×100%
=((6×6)/(5×5)-1)×100%
=11/25×100%=44%
Quantity Price
6 5
5 6
% profit = (xw/yz-1)×100%
=((6×6)/(5×5)-1)×100%
=11/25×100%=44%
DISHONEST DEALING
A merchant uses y% less weight/length and sells his good at gain/loss of x%. The overall % gain/loss is given by [((y+x)/(100-y))×100]%
Example 7:
A shopkeeper sells the goods at 44% loss on cost price but uses 30% less weight. What is his percentage profit or loss?
Solution:
Given, x = -44, y = 30
The overall % gain/loss = ((30-44)/(100-30)×100)% = -20%
Which represents loss being a negative expression.
A shopkeeper sells the goods at 44% loss on cost price but uses 30% less weight. What is his percentage profit or loss?
Solution:
Given, x = -44, y = 30
The overall % gain/loss = ((30-44)/(100-30)×100)% = -20%
Which represents loss being a negative expression.
Example 8:
A cloth merchant says that due to slump in the market, he sells the cloth at 10% loss, but he uses a false metre-scale and actually gain 15%. Find the actual length of the scale.
Solution:
(True Scale)/(False Scale)=(100+gain%)/(100-loss%)
100/(False Scale)=(100+15)/(100-10)
⇒False Scale=(100×90)/115=78.26cm
A cloth merchant says that due to slump in the market, he sells the cloth at 10% loss, but he uses a false metre-scale and actually gain 15%. Find the actual length of the scale.
Solution:
(True Scale)/(False Scale)=(100+gain%)/(100-loss%)
100/(False Scale)=(100+15)/(100-10)
⇒False Scale=(100×90)/115=78.26cm
Example 9:
A dishonest dealer professes to sell his goods at cost price, but he uses a weight of 960 g for the kg weight. Find his gain per cent.
Solution:
Error = 1 kg – 960g
= 1000g – 960 g = 40g.
∴Gain% = 40/(1000-40)×100
=40/960×100=41/6%
A dishonest dealer professes to sell his goods at cost price, but he uses a weight of 960 g for the kg weight. Find his gain per cent.
Solution:
Error = 1 kg – 960g
= 1000g – 960 g = 40g.
∴Gain% = 40/(1000-40)×100
=40/960×100=41/6%
GOODS PASSING THROUGH SUCCESSIVE HANDS
When there are two successive profits of a % and b%, then the resultant profit per cent is given by
(a+b+ab/100)%
When there is a profit of a % and loss by b % in a transaction, then the resultant profit or loss per cent is given by (a-b-ab/100)%, according to the ve or –ve sign respectively.
When cost price and selling price are reduced by the same amount (A) and profit increases then cost price (C.P.)
=[Initial profit %+Increase in profit %]×A]/(Increase in profit %)
When there are two successive profits of a % and b%, then the resultant profit per cent is given by
(a+b+ab/100)%
When there is a profit of a % and loss by b % in a transaction, then the resultant profit or loss per cent is given by (a-b-ab/100)%, according to the ve or –ve sign respectively.
When cost price and selling price are reduced by the same amount (A) and profit increases then cost price (C.P.)
=[Initial profit %+Increase in profit %]×A]/(Increase in profit %)
Example 10:
A table is sold at a profit of 20%. If the cost price and selling price are Rs 200 less, the profit would be 8% more. Find the cost price.
Solution:
By direct method,
C.P. = Rs ((20+8)×200)/8=Rs 28×25 = Rs 700
If cost price of x articles is equal to the selling price of y articles, then profit/loss percentage =(x-y)/y×100%, according to +ve or –ve sign respectively.
A table is sold at a profit of 20%. If the cost price and selling price are Rs 200 less, the profit would be 8% more. Find the cost price.
Solution:
By direct method,
C.P. = Rs ((20+8)×200)/8=Rs 28×25 = Rs 700
If cost price of x articles is equal to the selling price of y articles, then profit/loss percentage =(x-y)/y×100%, according to +ve or –ve sign respectively.
Example 11:
If the C.P. of 15 tables be equal to the S.P. of 20 tables, find the loss per cent.
Solution:
By direct method,
Profit/loss % = (-5)/20×100 = 25% loss, since it is –ve.
If the C.P. of 15 tables be equal to the S.P. of 20 tables, find the loss per cent.
Solution:
By direct method,
Profit/loss % = (-5)/20×100 = 25% loss, since it is –ve.
Example 12:
If the C.P. of 6 articles is equal to the S.P. of 4 articles. Find the gain per cent.
Solution:
Let C.P. of an article be Rs x; then,
C.P. of 6 articles = Rs 6x
C.P. of 4 articles = Rs 4x
But S.P. of 4 articles = C.P. of 6 articles
∴S.P. of 4 articles = 6x
Thus, gain = S.P. – C.P. = Rs (6x-4x) = Rs 2x
∴Gain % = 2x/4x×100 = 50
Thus, gain in the transaction = 50%
If the C.P. of 6 articles is equal to the S.P. of 4 articles. Find the gain per cent.
Solution:
Let C.P. of an article be Rs x; then,
C.P. of 6 articles = Rs 6x
C.P. of 4 articles = Rs 4x
But S.P. of 4 articles = C.P. of 6 articles
∴S.P. of 4 articles = 6x
Thus, gain = S.P. – C.P. = Rs (6x-4x) = Rs 2x
∴Gain % = 2x/4x×100 = 50
Thus, gain in the transaction = 50%
Example 13:
By selling 33 metres of cloth, a man gains the sale price of 11 metres. The gain % is
Solution:
Gain = S.P. of 33 metres – C.P. of 33 metres
= S.P. of 11 metres
⇒ S.P. of 22 metres = C.P. of 33 metres
∴% gain = gain/(C.P.of metres)×100
= (S.P.of 11 metres)/(C.P.of 33 metres)×100
= (S.P.of 11 metres)/(S.P.of 22 metres)×100=11/22×100 = 50%
By selling 33 metres of cloth, a man gains the sale price of 11 metres. The gain % is
Solution:
Gain = S.P. of 33 metres – C.P. of 33 metres
= S.P. of 11 metres
⇒ S.P. of 22 metres = C.P. of 33 metres
∴% gain = gain/(C.P.of metres)×100
= (S.P.of 11 metres)/(C.P.of 33 metres)×100
= (S.P.of 11 metres)/(S.P.of 22 metres)×100=11/22×100 = 50%
Shortcut method:
If on selling ‘x’ articles a man gains equal to the S.P. of y articles.
Then,
%gain=y/(x-y)×100=11/(33-11)×100=11/22×100=50%
Marked Price: The price on the lable is called the marked price.
The marked price is abbreviated as M.P.
Discount: The reduction made on the ‘marked price’ of an article is called the discount.
NOTE:
When no discount is given, ‘selling price’ is the same as ‘marked price’.
Discount = Marked price × Rate of discount.
S.P. = M.P. – Discount.
Discount% = Discount/(M.P.)×100
Buy x get y free i.e., if x + y articles are sold at cost price of x articles, then the percentage discount =y/(x+y)×100.
If on selling ‘x’ articles a man gains equal to the S.P. of y articles.
Then,
%gain=y/(x-y)×100=11/(33-11)×100=11/22×100=50%
Marked Price: The price on the lable is called the marked price.
The marked price is abbreviated as M.P.
Discount: The reduction made on the ‘marked price’ of an article is called the discount.
NOTE:
When no discount is given, ‘selling price’ is the same as ‘marked price’.
Discount = Marked price × Rate of discount.
S.P. = M.P. – Discount.
Discount% = Discount/(M.P.)×100
Buy x get y free i.e., if x + y articles are sold at cost price of x articles, then the percentage discount =y/(x+y)×100.
Example 14:
How much % must be added to the cost price of goods so that a profit of 20%must be made after throwing off a discount of 10% from the marked price?
Solution:
Let C.P. = Rs 100, then S.P. = Rs 120
Also, Let marked price be Rs x. Then
90% of x = 120 ⇒x=(120×100)/90=1331/3
∴ M.P. should be Rs 133 1/3
or M.P. = 33 1/3 % above C.P.
How much % must be added to the cost price of goods so that a profit of 20%must be made after throwing off a discount of 10% from the marked price?
Solution:
Let C.P. = Rs 100, then S.P. = Rs 120
Also, Let marked price be Rs x. Then
90% of x = 120 ⇒x=(120×100)/90=1331/3
∴ M.P. should be Rs 133 1/3
or M.P. = 33 1/3 % above C.P.
Example 15:
At a clearance sale, all goods are on sale at 45% discount. If I buy a skirt marked Rs600, how much would I need to pay?
Solution:
M.P. =Rs 600, Discount = 45%
Discount = (M.P.×Discount %)/100=(600×45)/100=Rs270.
∴ S.P. = M.P. – Discount
s.p =600-270=330. Hence the amount I held to pay is 330.Alternate method; s.p capital =M.P×0.55
= Rs 600× 0.55 = Rs 330
A man purchases a certain number of articles at x a rupee and the same number at y a rupee. He mixes them together and sells them at z a rupee. then his gain or loss %
=[2xy/z(x+y) -1]×100 according as the sign is +ve or –ve.
If two items are sold, each at Rs x, one at a gain of p% and the other at a loss of p%, there is an overall loss given byp^2/100%.
Note that in such cases there is always a loss.
The absolute value of the loss is given by (〖2p〗^2 x)/(〖100〗^2-p^2 )
If CP of two items is the same and % Loss and % Gain on the two items are equal, then net loss or net profit is zero.
At a clearance sale, all goods are on sale at 45% discount. If I buy a skirt marked Rs600, how much would I need to pay?
Solution:
M.P. =Rs 600, Discount = 45%
Discount = (M.P.×Discount %)/100=(600×45)/100=Rs270.
∴ S.P. = M.P. – Discount
s.p =600-270=330. Hence the amount I held to pay is 330.Alternate method; s.p capital =M.P×0.55
= Rs 600× 0.55 = Rs 330
A man purchases a certain number of articles at x a rupee and the same number at y a rupee. He mixes them together and sells them at z a rupee. then his gain or loss %
=[2xy/z(x+y) -1]×100 according as the sign is +ve or –ve.
If two items are sold, each at Rs x, one at a gain of p% and the other at a loss of p%, there is an overall loss given byp^2/100%.
Note that in such cases there is always a loss.
The absolute value of the loss is given by (〖2p〗^2 x)/(〖100〗^2-p^2 )
If CP of two items is the same and % Loss and % Gain on the two items are equal, then net loss or net profit is zero.
Example 16:
A shopkeeper sold two radio sets for Rs 792 each, gaining 10% on one, and losing 10% on the other. Then he
Solution:
When selling price of two articles is same and % gain = % loss
then there will be always loss.
and overall % loss = (10)^2/100%= 1%
A shopkeeper sold two radio sets for Rs 792 each, gaining 10% on one, and losing 10% on the other. Then he
Solution:
When selling price of two articles is same and % gain = % loss
then there will be always loss.
and overall % loss = (10)^2/100%= 1%
Example 17:
A man bought two housing apartments for Rs2 lakhs each. He sold one at 20% loss and the other at 20% gain. Find his gain or loss.
Solution:
When C.P. of two articles is same and
% gain = % loss
Then, on net, there is no loss, no gain
If an article is sold at a price S.P1…, then % gain or % loss is x and if it is sold at a price S.P2… then % gain or % loss is y. If the cost price of the article is C.P., then
〖S.P〗_1/(100+x)=〖S.P〗_2/(100+y)=(C.P.)/100=(〖S.P〗_1-〖S.P〗_2)/(x-y)
where x or y is negative, if in indicates a loss, otherwise it is positive.
A man bought two housing apartments for Rs2 lakhs each. He sold one at 20% loss and the other at 20% gain. Find his gain or loss.
Solution:
When C.P. of two articles is same and
% gain = % loss
Then, on net, there is no loss, no gain
If an article is sold at a price S.P1…, then % gain or % loss is x and if it is sold at a price S.P2… then % gain or % loss is y. If the cost price of the article is C.P., then
〖S.P〗_1/(100+x)=〖S.P〗_2/(100+y)=(C.P.)/100=(〖S.P〗_1-〖S.P〗_2)/(x-y)
where x or y is negative, if in indicates a loss, otherwise it is positive.
Example 18:
By selling a radio for Rs 1536, Ramesh lost 20%. What per cent shall he gain or lose by selling it for Rs 2000?
Solution:
Given, S.P1 = 1536, x = -20 (-ve sign indicates loss)
S.P2 = Rs 2000, y =?
Using the formula,
〖S.P〗_1/(100+x)=〖S.P〗_2/(100+y)
we get 1536/(100-20)=2000/(100+y)
⇒100+y= (2000×80)/1536=1041/6
⇒y=41/6 %
Thus, Ramesh has a gain of 41/6% by selling it for Rs 2,000
It A sells an article to B at a gain/loss of m% and B sells it to C at a gain/loss of n%. If C pays Rs z for it to B then the cost
price for A is [(〖100〗^2 z)/((100+m)(100+n))]
Where m or n is negative, of it indicates a loss, otherwise it positive.
By selling a radio for Rs 1536, Ramesh lost 20%. What per cent shall he gain or lose by selling it for Rs 2000?
Solution:
Given, S.P1 = 1536, x = -20 (-ve sign indicates loss)
S.P2 = Rs 2000, y =?
Using the formula,
〖S.P〗_1/(100+x)=〖S.P〗_2/(100+y)
we get 1536/(100-20)=2000/(100+y)
⇒100+y= (2000×80)/1536=1041/6
⇒y=41/6 %
Thus, Ramesh has a gain of 41/6% by selling it for Rs 2,000
It A sells an article to B at a gain/loss of m% and B sells it to C at a gain/loss of n%. If C pays Rs z for it to B then the cost
price for A is [(〖100〗^2 z)/((100+m)(100+n))]
Where m or n is negative, of it indicates a loss, otherwise it positive.
Example 19:
Mohit sells a bicycle to Rohit at a gain of 10% and Rohit again sells it to Jyoti at a profit of 5%. If Jyoti pays Rs 462 to Rohit. What is the cost price of the bicycle for Mohit.
Solution:
Given, m = 10, n = 5, z = Rs 462
Using the formula, C.P. =[(〖100〗^2 z)/((100+m)(100+n))]
we get C.P. for Mohit = [(〖100〗^2×462)/((100+10)(100+5))]
When two different articles sold at same S.P. x and y are % gain (or loss) on them. Then overall % gain or loss
=[(100(x+y)+2xy)/((100+x)(100+y))]
The above expression represent overall gain or loss according to its sign.
Mohit sells a bicycle to Rohit at a gain of 10% and Rohit again sells it to Jyoti at a profit of 5%. If Jyoti pays Rs 462 to Rohit. What is the cost price of the bicycle for Mohit.
Solution:
Given, m = 10, n = 5, z = Rs 462
Using the formula, C.P. =[(〖100〗^2 z)/((100+m)(100+n))]
we get C.P. for Mohit = [(〖100〗^2×462)/((100+10)(100+5))]
When two different articles sold at same S.P. x and y are % gain (or loss) on them. Then overall % gain or loss
=[(100(x+y)+2xy)/((100+x)(100+y))]
The above expression represent overall gain or loss according to its sign.
Example 20:
A man sold two watches for ` 1000 each. On one he gains 25% and on the other 20% loss. Find how much % does he gain or loss in the whole transaction?
Solution:
When S1 = S2, then
overall % gain or % loss
=((100(x+y)+2xy)/((100+x)+(100+y)))
=((100(25-20)+2×25×-20)/((100+25)+(100-20)) ))
=-100/41% loss (∵ it is –ve)
A man sold two watches for ` 1000 each. On one he gains 25% and on the other 20% loss. Find how much % does he gain or loss in the whole transaction?
Solution:
When S1 = S2, then
overall % gain or % loss
=((100(x+y)+2xy)/((100+x)+(100+y)))
=((100(25-20)+2×25×-20)/((100+25)+(100-20)) ))
=-100/41% loss (∵ it is –ve)
Example 21:
After allowing a discount of 12% on the marked price of an article, it is sold for `880. Find its marked price.
Solution:
S.P. = `880 and Discount % = 12
Let M.P. =x
Discount = (M.P.×Discount%)/100=(x×12)/100=3/25 x
Now, M.P. = S.P. + Discount
x =880 + 3/25x
⇒x-3/25 x=880 ⇒22x/25=880
⇒x= (880×25)/22=40×25 = `1000
∴ Marked price of the article is `1000
After allowing a discount of 12% on the marked price of an article, it is sold for `880. Find its marked price.
Solution:
S.P. = `880 and Discount % = 12
Let M.P. =x
Discount = (M.P.×Discount%)/100=(x×12)/100=3/25 x
Now, M.P. = S.P. + Discount
x =880 + 3/25x
⇒x-3/25 x=880 ⇒22x/25=880
⇒x= (880×25)/22=40×25 = `1000
∴ Marked price of the article is `1000
Example 22:
A shopkeeper offers his customers 10% discount and still makes a profit of 26%. What is the actual cost to him of an article marked `280?
Solution:
M.P. = `280 and Discount % = 10
Discount = (M.P.×Discount%)/100=(280×10)/100=`28
S.P. =M.P. – Discount = `280- `252
Now, S.P. = `252 and profit = 26%
∴ C.P. = 100/(100+Profit %)×S.P.
=100/(100+26)×252=`200
Hence, the actual cost of the article is `200.
A shopkeeper offers his customers 10% discount and still makes a profit of 26%. What is the actual cost to him of an article marked `280?
Solution:
M.P. = `280 and Discount % = 10
Discount = (M.P.×Discount%)/100=(280×10)/100=`28
S.P. =M.P. – Discount = `280- `252
Now, S.P. = `252 and profit = 26%
∴ C.P. = 100/(100+Profit %)×S.P.
=100/(100+26)×252=`200
Hence, the actual cost of the article is `200.
SUCCESSIVE DISCOUNT:
In successive discounts, first discount is subtracted from the marked price to get net price after the first discount. Taking this price as the new marked price, the second discount is calculated and it is subtracted from it to get net price after the second discount. Continuing in this manner, we finally obtain the net selling price.
In case of successive discounts a % and b%, the effective discount is (a+b-ab/100)%
In successive discounts, first discount is subtracted from the marked price to get net price after the first discount. Taking this price as the new marked price, the second discount is calculated and it is subtracted from it to get net price after the second discount. Continuing in this manner, we finally obtain the net selling price.
In case of successive discounts a % and b%, the effective discount is (a+b-ab/100)%
Example 23:
Find the single discount equivalent to successive discounts of 15% and 20%
Solution:
By direct formula,
Single discount = (a+b-ab/100)%
=(15+20-(15×20)/100)%=32%
If three or more successive discounts on an article are a%, b%, c% and respectively then a single discount to the successive discounts will be
[1-(1-(a%)/100)(1-(b%)/100)(1-(c%)/100)(1-(d%)/100) ]%
Find the single discount equivalent to successive discounts of 15% and 20%
Solution:
By direct formula,
Single discount = (a+b-ab/100)%
=(15+20-(15×20)/100)%=32%
If three or more successive discounts on an article are a%, b%, c% and respectively then a single discount to the successive discounts will be
[1-(1-(a%)/100)(1-(b%)/100)(1-(c%)/100)(1-(d%)/100) ]%
Example 24:
Find single equivalent discount of successive discount of 30%, 20%, 40% and 10%.
Solution:
Single discount = [1-(1-30) × (1-20) × (1-40)× (1-10)×100] = 69.76%
Find single equivalent discount of successive discount of 30%, 20%, 40% and 10%.
Solution:
Single discount = [1-(1-30) × (1-20) × (1-40)× (1-10)×100] = 69.76%
Example 25:
Find the S.P. of an article whose M.P. is `9988467 giving successive discount of 50%, 40% and 10%.
Solution:
Equivalent discount = [1-(.50×.60×.90) ×100] =73%
S.P. =9988467 × (100-73)/100 = 2696886.09
Find the S.P. of an article whose M.P. is `9988467 giving successive discount of 50%, 40% and 10%.
Solution:
Equivalent discount = [1-(.50×.60×.90) ×100] =73%
S.P. =9988467 × (100-73)/100 = 2696886.09
Example 26:
If an article is marked at `1000000, and on purchasing a person gets discount of 30%, 30%, 20%, 10% and 10% successively. Find his over all discount percentage.
Solution:
[1-(.07×.07×.08×.09×.09)] × 100 = 68.24%
If an article is marked at `1000000, and on purchasing a person gets discount of 30%, 30%, 20%, 10% and 10% successively. Find his over all discount percentage.
Solution:
[1-(.07×.07×.08×.09×.09)] × 100 = 68.24%
Example 27:
An article is listed at `65. A customer bought this article for `56.16 and got successive discounts of which the first one is 10%. The other rate of discount of this scheme that was allowed by the shopkeeper was:
Solution:
Price of the article after discount 65 – 6.5 = `58.5
Therefore, the second discount
= (58.5-56.16)/58.5×100=4%
An article is listed at `65. A customer bought this article for `56.16 and got successive discounts of which the first one is 10%. The other rate of discount of this scheme that was allowed by the shopkeeper was:
Solution:
Price of the article after discount 65 – 6.5 = `58.5
Therefore, the second discount
= (58.5-56.16)/58.5×100=4%
Example 28:
A shopkeeper offers 5% discount on all his goods to all his customers. He offers a further discount of 2% on the reduced price to those customers who pay cash. What will you actually have to pay for an article in cash if its M.P. is `4800?
Solution:
M.P. = `4800
First discount = 5% of M.P.
= 5/100×4800= `240
Net price after discount = `4800 – `240
= `4560
Second discount = 2% of `4560
= 2/100×4560= `91.20
Net price after discount = ` 4560 – ` 91.20
= `4468.80
By Direct Method:
S.P. = 4800 (1-5/100)(1-2/100)=`4468.80
A person buys two items for ` A and sells one at a loss of l% and other at a gain of g%. If each item was sold at the same price, then
(a) The cost price of the items sold at loss
= (A (100+%gain))/((100-%loss)+(100+%gain))
(b) The cost price of the item sold at gain
= (A (100+%loss))/((100-%loss)+(100+%gain))
A shopkeeper offers 5% discount on all his goods to all his customers. He offers a further discount of 2% on the reduced price to those customers who pay cash. What will you actually have to pay for an article in cash if its M.P. is `4800?
Solution:
M.P. = `4800
First discount = 5% of M.P.
= 5/100×4800= `240
Net price after discount = `4800 – `240
= `4560
Second discount = 2% of `4560
= 2/100×4560= `91.20
Net price after discount = ` 4560 – ` 91.20
= `4468.80
By Direct Method:
S.P. = 4800 (1-5/100)(1-2/100)=`4468.80
A person buys two items for ` A and sells one at a loss of l% and other at a gain of g%. If each item was sold at the same price, then
(a) The cost price of the items sold at loss
= (A (100+%gain))/((100-%loss)+(100+%gain))
(b) The cost price of the item sold at gain
= (A (100+%loss))/((100-%loss)+(100+%gain))
Example 29:
Ramesh buys two books for `410 and sells one at a loss of 20% and the other at a gain of 25%. If both the books are sold at the same price. Find the cost price of two books.
Solution:
Give, A = 410
Cost price of the books sold at loss = ((410)(100+25))/((100-20)+(100+25))
= (410×125)/(80+125)= `250/-
Cost price of the books sold at profit
= ((410)(100-20))/((100-20)+(100+25))
= (410×80)/(80+125) = `160/-
Ramesh buys two books for `410 and sells one at a loss of 20% and the other at a gain of 25%. If both the books are sold at the same price. Find the cost price of two books.
Solution:
Give, A = 410
Cost price of the books sold at loss = ((410)(100+25))/((100-20)+(100+25))
= (410×125)/(80+125)= `250/-
Cost price of the books sold at profit
= ((410)(100-20))/((100-20)+(100+25))
= (410×80)/(80+125) = `160/-
SALES TAX
To meet government’s expenditures like construction of roads, railway, hospitals, schools etc, the government imposes different types of taxes. Sales tax
(S.T.) is one of these tax.
Sales tax is calculated on selling price (S.P.)
To meet government’s expenditures like construction of roads, railway, hospitals, schools etc, the government imposes different types of taxes. Sales tax
(S.T.) is one of these tax.
Sales tax is calculated on selling price (S.P.)
NOTE:
If discount is given, selling price is calculated first and then sales tax is calculated on the selling price of the article.
Example 30:
Sonika bought a V.C.R. at the list price of `18,500. If the rate of sales tax was 8%, find the amount she had to pay for purchasing the V.C.R.
Sonika bought a V.C.R. at the list price of `18,500. If the rate of sales tax was 8%, find the amount she had to pay for purchasing the V.C.R.
Solution:
List price of V.C.R. = `18,500
Rate of sales tax = 8%
∴ Sales tax = 8% of `18,500
= 8/100×18500= `1480
So, total amount which Sonika had to pay for purchasing the V.C.R. = `18,500 + `1480
= `19,980
List price of V.C.R. = `18,500
Rate of sales tax = 8%
∴ Sales tax = 8% of `18,500
= 8/100×18500= `1480
So, total amount which Sonika had to pay for purchasing the V.C.R. = `18,500 + `1480
= `19,980
Example 31:
The sale price of an article including the sales tax is `616. The rate of sales tax is 10%. If the shopkeeper has made a profit of 12%, then the cost price of the article is:
Solution:
Let the CP of the article be `x
Then, SP = x × 1.12 × 1.1
Now, x ×1.12×1.1-616
⇒ x = 616/1.232=`500
The sale price of an article including the sales tax is `616. The rate of sales tax is 10%. If the shopkeeper has made a profit of 12%, then the cost price of the article is:
Solution:
Let the CP of the article be `x
Then, SP = x × 1.12 × 1.1
Now, x ×1.12×1.1-616
⇒ x = 616/1.232=`500
Example 32:
Pure ghee cost ` 100 per kg. After adulterating it with vegetable oil costing `50 per kg, a shopkeeper sells the mixture at the rate of ` 96 per kg, thereby making a profit of 20%. In what ratio does he mix the two?
Solution:
Mean cost price = ` (100/120×96) = `80 per kg.
By the rule of allegation:
C.P. of 1 kg ghee
Pure ghee cost ` 100 per kg. After adulterating it with vegetable oil costing `50 per kg, a shopkeeper sells the mixture at the rate of ` 96 per kg, thereby making a profit of 20%. In what ratio does he mix the two?
Solution:
Mean cost price = ` (100/120×96) = `80 per kg.
By the rule of allegation:
C.P. of 1 kg ghee
∴ Required ratio = 30:20=3:2
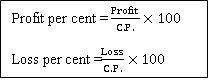
Comments
Post a Comment